El propósito del tutorial es que, con base en los temas vistos en la semana anterior, se construya un modelo a partir de la situación que se plantea y se diligencie el Formato de control de experimentos en la medida en que se le indica. Este tutorial les servirá además para crear otros modelos y simulaciones relacionadas con otras situaciones de su interés.

Este tutorial presenta el proceso para la construcción y simulación de un modelo de Dinámica de Sistemas a partir de un caso de la dinámica entre una población de zorros y una de conejos. Se basa en algunas publicaciones del grupo de Dinámica de Sistemas del MIT. Está basado en: Modeling Exercises Joseph Whelan, MIT System Dynamics Education Project 1994 & Business Dynamics, John Sterman, 2000.

¿Qué necesita?

1. Descargar e instalar la versión "PLE" (Personal Learning Edition) del software Vensim. Las instrucciones detalladas se encuentran en el "Tutorial de Vensim: Realimentación" de la semana 1.

2. Descargar el Formato de registro de experimentos disponible aquí (haciendo click derecho en el siguiente enlace): Formato Experimentos. En este formato debe ir registrando los resultados que obtenga a lo largo de la construcción del modelo. No es necesario que entregue este formato diligenciado, es una herramienta de apoyo para la construcción del modelo y diligenciamiento de resultados.

Las variaciones de poblaciones que no son debidas a cambios periódicos evidentes (por ejemplo las estaciones) sino que incluyen ciclos regulatorios de abundancia y escasez, con picos y depresiones cada cierto tiempo, son poco comprendidas. Los casos más conocidos ocurren con mamíferos, aves, insectos y peces. Entre los mamíferos los casos más estudiados exhiben periodicidades de 9 a 10 años o de 3 a 4 años. Por lo general picos de abundancia en el tamaño de la población son seguidos por descensos vertiginosos. Es necesario comprender sistémicamente estas dinámicas, lo que quiere decir establecerlas como resultado de las operaciones que ocurren dentro del sistema y la forma cómo éste está organizado—en lugar de entenderlas en función de factores exógenos como cambios climáticos o la influencia de agentes externos.

Considere un bosque con un área de 1000 hectáreas, cerca de la región polar ártica, en el que una población de zorros del ártico y una de conejos interactúan constantemente. Los zorros de esta especie son especialistas y se alimentan exclusivamente de carne y por lo tanto su supervivencia depende de los conejos ya que son la única presa a su disposición. Estudios recientes calcularon que en el año 2000 había 1250 zorros y 50000 conejos. La fracción de nacimientos de los zorros se estimó en 0.25 cada año (es decir, 25% anual, como porcentaje de la población). La tasa de nacimientos de conejos es considerablemente superior, de hecho está calculada en 1.25 al año.

La fracción de muerte anual de los depredadores (los zorros) depende de la densidad de población de la presa (los conejos) de acuerdo con los valores de la Tabla 1. Para modelar relaciones no lineales entre variables, como en este caso, podemos utilizar "funciones tabla" (denominadas también "Funciones gráficas o "Funciones Lookup"); estas nos permiten expresar una relación entre dos variables con diferentes formas y características especiales definiendo puntos de la función con tuplas o pares ordenados (x, y); el primer valor es la entrada y el segundo valor es la salida de la función; los paquetes de software de Dinámica de Sistemas típicamente interpolan linealmente los valores intermedios.

La densidad de conejos es igual a la cantidad de conejos por hectárea (es decir: conejos / área); es conveniente definir explícitamente el área de bosque como variable auxiliar para poderla eventualmente manipular en caso de querer analizar variaciones en dicha área. Cuando no hay conejos, los zorros mueren muy rápidamente a una tasa del 50% anual; a medida que la densidad de conejos aumenta, la población de zorros que muere por hambre disminuye hasta que la fracción de muertes de éstos llega a 0.0725. La Tabla 1 muestra que la fracción de muertes anuales de los depredadores cambia ampliamente de acuerdo con la cantidad de conejos disponible. Cuando el número de presas en el área es pequeño, los zorros no alcanzan a cazar todo lo que necesitan y su supervivencia declina; cuando no hay conejos los zorros mueren a una tasa que es el doble de la de nacimientos. Con una mayor densidad de conejos la fracción de muertes de zorros es menor.

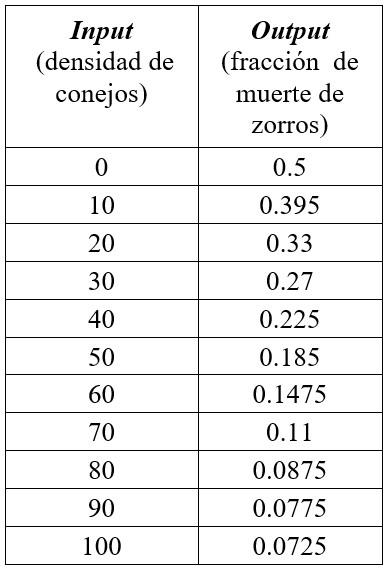
Tabla 1.

Fracción de muertes de zorros según la densidad de conejos

Por ahora únicamente vamos a considerar la muerte de los conejos ocasionadas por la cacería que les hacen los zorros; las muertes por otras razones (enfermedades, edad, etc.) no se tendrán en cuenta. La cantidad de presas que caza un zorro varía según la densidad de población de conejos, tal como lo muestra la Tabla 2. Cuando no hay conejos los zorros evidentemente no capturan ningún conejo. A medida que la densidad de conejos es mayor, entonces también la tasa de capturas por zorro es más alta hasta un límite de 500 conejos que es la cantidad máxima que un zorro podría alcanzar a consumir en un año; llega un punto en que la densidad de conejos es suficiente y los zorros no necesitan alimentarse más, así la abundancia de conejos sea considerable.

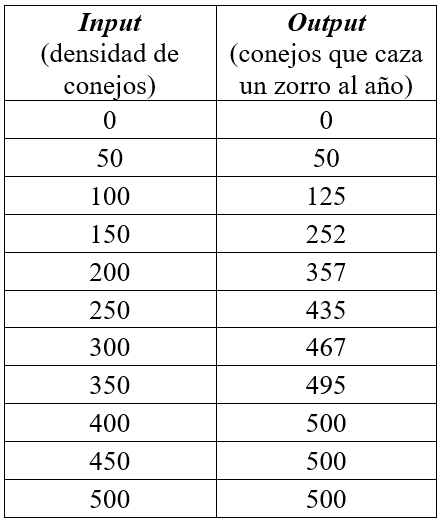
Tabla 2. Conejos que casa un zorro anualmente según la densidad de conejos

La información anterior es suficiente para construir un modelo dinámico que capture la mutua interdependencia de las dos poblaciones. Este tipo de modelos se conocen como "sistemas predador-presa Lotka-Volterra", propuestos por primera vez en 1925 por Alfred Lotka y Vito Volterra, y han sido utilizados como base para estudiar dinámicas poblacionales en biología; también se han utilizado en otras aplicaciones, por ejemplo juegos como SimCity o Ultima Online, para modelar poblaciones interdependientes.

A partir de la situación descrita anteriormente se puede construir un modelo dinámico que capture la mutua interdependencia de las dos poblaciones. Para construir el modelo de zorros y conejos se pueden construir dos modelos simples de población y conectarlos para que sean interdependientes a partir de las relaciones operacionales entre ambas poblaciones. Para lograr dicho modelo se debe:

1. Identificar las variables a considerar. ¿Cuáles deberían ser los niveles?, ¿cuáles deberían ser flujos? y ¿cuáles serían variables auxiliares?

2. Definir el horizonte de tiempo y la unidad de tiempo de simulación.

3. Mapear el modelo en Vensim como un modelo de niveles y flujos. Por ejemplo, puede primero mapear el modelo de la población de zorros, luego la de conejos y finalmente, definir cómo se relacionan entre sí.

4. Especificar los valores de las constantes (incluyendo valores iniciales de los niveles).

5. Definir las ecuaciones de todas las variables del modelo. Algunas ecuaciones deberán definirse como "funciones tabla", para esto:

a. En el cuadro de diálogo de la ecuación de una variable auxiliar defina su tipo ("Type") como "Auxiliary" (1) y su sub-tipo ("Sub-Type") como "with Lookup" (2).

b. En el recuadro de ecuaciones (3) especifique la variable de entrada de la función (e.g. para la fracción de muertes de zorros sería la densidad de conejos) que se puede seleccionar de la lista de variables disponibles (4) en caso de que ya haya sido conectada con algún enlace de información.

c. Al escoger el sub-tipo "with Lookup" aparece el botón "As Graph" al lado derecho (5), oprímalo.

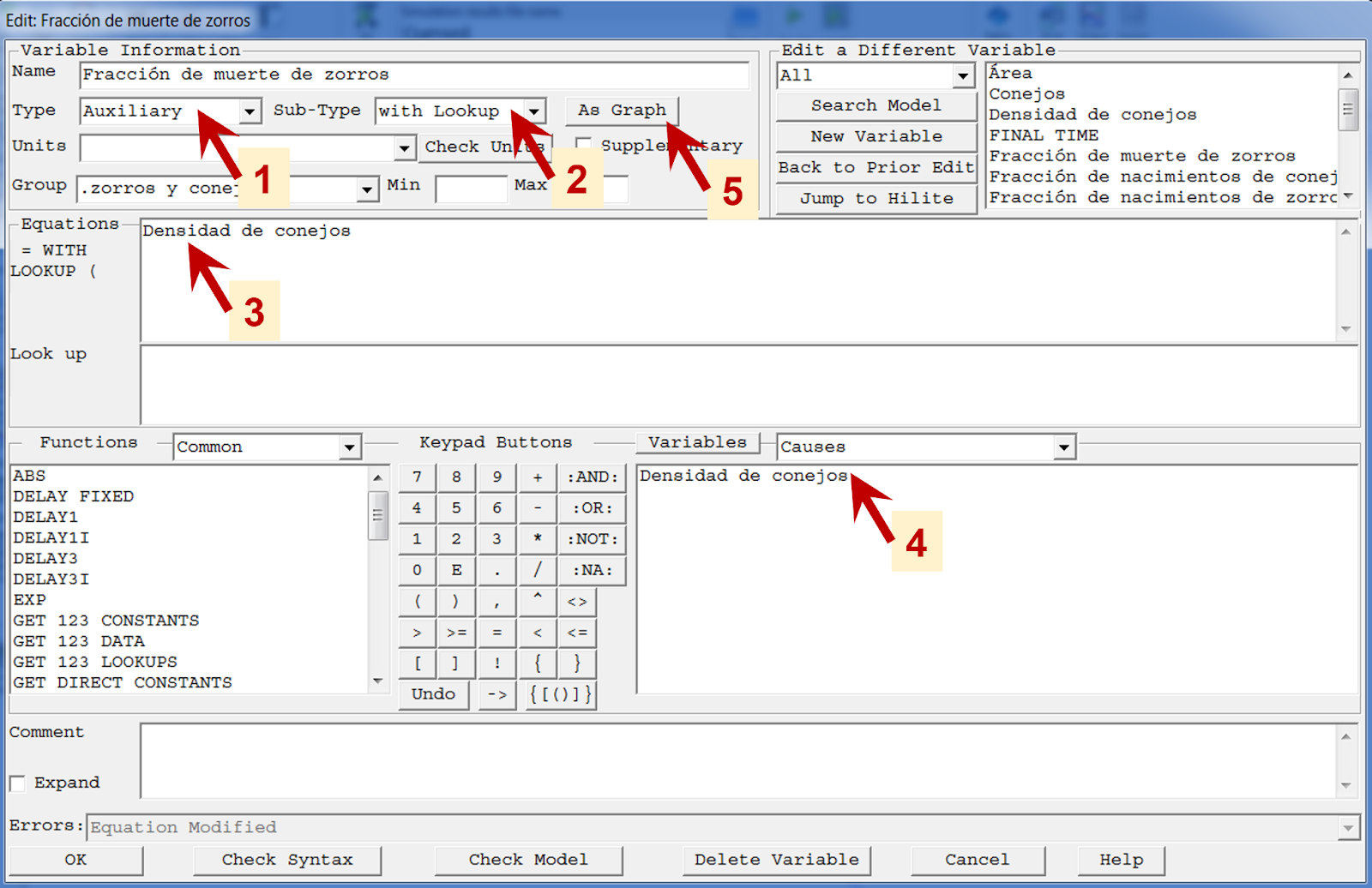
Imagen 1. Definición de funciones tabla.

d. Al hacer click en el botón "As Graph" se despliega un nuevo cuadro de diálogo para definir los valores de la entrada (en el caso de la fracción de muertes de zorros entonces la entrada es la densidad de conejos) y de la salida de la función (es decir, la fracción de muertes de zorros). Para apreciar la forma de la función es deseable ajustar los valores mínimos y máximos en los ejes X y Y para que correspondan con los límites extremos de los valores que tenemos disponibles; por ejemplo, para la fracción de muertes de zorros el valor máximo en el eje Y debería ser 0.5. Este cuadro de diálogo permite además definir los valores de la tabla también directamente sobre la misma gráfica de puntos haciendo click en los valores, esto para darle la forma deseada a la función, concepto que es necesario desarrollar para la construcción de modelos de Dinámica de Sistemas (más que los valores precisos de puntos y pares ordenados lo que nos interesa es la forma de la función).

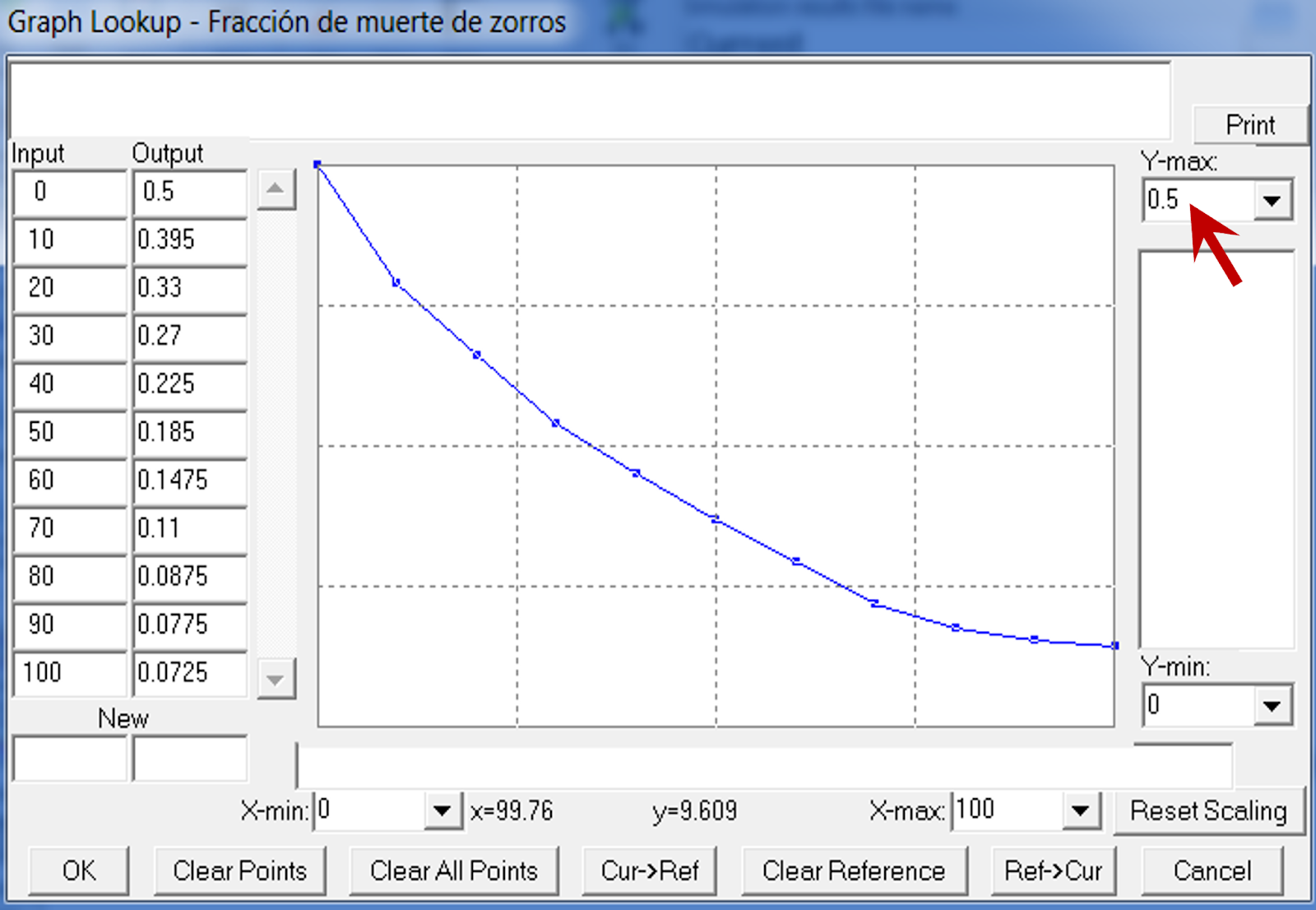
Imagen 2. Fracción de muerte de zorros como una función tabla.

Asegúrese de incluir todas las variables y definir sus ecuaciones en su modelo de Vensim teniendo en cuenta la información de la sección anterior de "Zorros y conejos" antes de pasar a la siguiente sección de "Simulación".

  1. Estimación del comportamiento pre-simulación

Antes de correr el modelo estime el comportamiento que seguirán las poblaciones.

  1. Simulación

Simule el modelo. Tenga en cuenta que al realizar las simulaciones Vensim puede reportar varias advertencias ("warnings") cuando algunas funciones tabla toman valores por fuera de los que especificamos explícitamente en los pares ordenados respectivos; esto no es problemático siempre y cuando el modelador sea consciente de estas implicaciones (más adelante, al momento de calibrar un modelo nos interesará especificar correctamente los límites mínimos y máximos de las funciones tabla de manera que al momento de realizar las simulaciones las funciones tomen valores dentro de los rangos que especificamos).

Imagen 3. Mensaje de "warning" que se despliega cuando alguna función toma valores por fuera de lo especificado.

¿Cuál es el comportamiento de las poblaciones? ¿Por qué? Caracterice estos comportamientos con los aspectos que Ud. considere son suficientes para esto, e.g. amplitud, período, frecuencia, estabilidad/inestabilidad, etc. Puede ser útil crear una gráfica en el panel de control que despliegue simultáneamente las poblaciones de zorros y de conejos. Tenga en cuenta también definir correctamente las unidades de tiempo del modelo (en este caso, años).

Incluya los resultados en el Formato de control de experimentos en la columna de "Resultado post-simulación" para la simulación "1. Zorros y conejos" en la variable correspondiente.

  1. Comportamiento del sistema en función de su estructura

Salvo que los parámetros y constantes tomen valores extremos o irreales, el patrón de comportamiento de las poblaciones de zorros y conejos no varía conceptualmente; varían algunos de sus atributos (e.g. amplitudes, períodos, etc.) pero no los patrones de comportamiento. Explore con SyntheSim variaciones "realistas" (es decir, que tomen valores razonables) para las constantes del modelo y el impacto que esto puede tener en el comportamiento del modelo. Por ejemplo, ¿en un área de bosque más grande (e.g. 2000 hectáreas) se esperaría que una mayor población de conejos conduzca a una sobrepoblación que crezca indefinidamente?

Comprender que es el mismo sistema el que produce endógenamente su propio comportamiento (antes que factores exógenos) es una de las claves conceptuales de la Dinámica de Sistemas y del pensamiento sistémico que ésta desarrolla y nos permite mejorar la calidad de nuestras explicaciones y la forma cómo entendemos un sistema de manera que podamos modificarlo y mejorar su desempeño. Anote sus explicaciones u observaciones sobre el patrón de comportamiento de estas poblaciones en el Formato de registro de experimentos en la columna de "Observaciones/explicaciones/hipótesis" respectivamente para cada variable.

  1. Funciones especiales

La piel del zorro del ártico es codiciada en el mercado negro. Suponga que en el año 2015 se estableció en el bosque una legión de cazadores furtivos y acabaron con la mitad de la población de zorros que había ese año. ¿Podría estimar el nuevo comportamiento de las poblaciones sin utilizar el computador? Anote su estimación en la columna de "Estimación pre-simulación" en el Formato de Control de experimentos en la simulación "2. Caza de zorros" para la variable correspondiente.

Los paquetes de software de Dinámica de Sistemas traen librerías de funciones adicionales (matriciales, estadísticas, lógicas, financieras, económicas, entre otras) que nos ayudan a ampliar nuestras posibilidades de modelado y análisis. Para el caso de los cazadores implemente en el modelo el evento anterior de los cazadores y compare los resultados con sus estimaciones. Utilice la función PULSE de Vensim para especificar y simular este evento (se puede utilizar por ejemplo en el flujo de muertes de zorros; también podría definirse un flujo de salida adicional nuevo). El cuadro de diálogo para definir la ecuación de una variable despliega posibles funciones disponibles junto con sus parámetros de entrada o consulte el menú de ayuda de Vensim para encontrar cómo especificar la función PULSE y para explorar otras funciones. Igualmente considere la configuración del modelo para que las simulaciones comiencen en t = 2000 (el año para el cual tenemos los valores iniciales) y un horizonte de por ejemplo 40 años y así implementar el evento de los cazadores para el año 2015.

Incluya los resultados en el Formato de control de experimentos en la columna de "Resultado post-simulación" para la simulación "2. Caza de zorros" en la variable correspondiente.

  1. Condiciones extremas

Hay diversas pruebas para evaluar la confiabilidad de un modelo, por ejemplo, qué tan confiables son sus resultados, qué tan confiable es su estructura, etc. Una prueba básica es examinar los resultados de las simulaciones cuando algunas de las variables toman valores extremos; el modelador debe tener claridad de cuáles deberían ser los valores que el modelo debería tomar en dichos casos extremos y el modelo efectivamente debe evidenciar esa robustez y arrojar los resultados esperados. Por ejemplo, ¿qué pasaría si la fracción de nacimientos de zorros llegara a cero? ¿Qué debería pasar con la población de zorros? ¿Y con la de conejos? Anote sus estimaciones en la columna de "Estimación (pre-simulación)" del Formato de control de experimentos, en la simulación "3. Condiciones extremas" para la variable correspondiente.

Ahora utilice SyntheSim para examinar el comportamiento de las poblaciones si la fracción de nacimientos de zorros toma el valor de cero. Incluya los resultados en el Formato de control de experimentos en la columna de "Resultado post-simulación" para la simulación "3. Condiciones extremas" para la variable correspondiente.

¿Se comporta el modelo de la manera esperada? ¿Son los resultados de los comportamientos de las poblaciones de zorros y de conejos coherentes con los valores que esperábamos que tomaran? Si es así se puede afirmar entonces que el modelo es robusto en condiciones extremas y por lo tanto nuestra confianza en él aumenta. Si los resultados no corresponden a las expectativas entonces tendremos que ajustar necesariamente una de dos cosas: nuestras expectativas (y a esto lo podemos llamar "aprendizaje") o el modelo (y a esto lo podemos llamar "calibración del modelo"); este último proceso (calibración) debe ser continuo e iterativo y se compone también de otras pruebas adicionales además de la prueba de condiciones extremas. Anote sus explicaciones u observaciones sobre el patrón de comportamiento de estas poblaciones en el Formato de registro de experimentos en la columna de "Observaciones/explicaciones/hipótesis" para la simulación "3. Condiciones extremas" respectivamente para cada variable.

  1. Error de integración

Vensim utiliza diferentes métodos de integración y diferentes diferenciales de tiempo (DT o TIME STEPS) para resolver las ecuaciones. El cambio en el método de integración implica el uso de diferentes técnicas de integración de diferente orden (Euler o Runge-Kutta 4) y el cambio en el DT implica que el simulador calcula los valores en intervalos de tiempo diferentes (1, 0.5, 0.25, 0.125, 0.0625, 0.0325, etc.) entre menor sea el valor del DT las simulaciones serán más precisas, pero también requerirán de mayor capacidad computacional. En el Tutorial de Vensim de la semana 3 aprendimos a modificar las configuraciones del modelo. Pruebe varias simulaciones y compárelas (utilizando "Graph" por ejemplo para alguna variable de interés) con diferentes valores de DT (siempre inferiores a 1) y diferentes métodos de integración. Incluya los resultados en el Formato de control de experimentos en la columna de "Resultado post-simulación" para la simulación "4. Error de integración" para la variable correspondiente.

¿Varían los resultados según el valor del DT o el método de integración? ¿De ser así con qué valor de DT y/o qué método de integración debería utilizar este modelo? ¿Por qué? Anote sus explicaciones u observaciones sobre el patrón de comportamiento de estas poblaciones en el Formato de registro de experimentos en la columna de "Observaciones/explicaciones/hipótesis" para la simulación "4. Error de integración" respectivamente para cada variable.

  1. Análisis de sensibilidad

El análisis de sensibilidad se puede llevar a cabo para evaluar aquellos parámetros del modelo sobre los que existe alguna incertidumbre. Este tipo de experimentos busca evaluar los resultados que se producen al variar los parámetros dentro de un rango sobre el que se cree se puede variar. Se pueden apreciar tres tipos de sensibilidad en un modelo:

- Sensibilidad numérica: se presenta cuando cambios en supuestos, frontera, nivel de agregación, parámetros o variables afectan significativamente los valores numéricos de las simulaciones de nuestras variables de interés pero no necesariamente sus patrones de comportamiento. Un patrón de comportamiento podría mantenerse como tal, e.g. oscilatorio, con cambios únicamente numéricos (e.g. cambios en la frecuencia, período o en la amplitud de las oscilaciones). Esta sensibilidad es característica de todos los modelos.

- Sensibilidad en comportamiento: se presenta cuando cambios en supuestos, frontera, nivel de agregación, parámetros o variables alteran significativamente los patrones de comportamiento de nuestras variables de interés (e.g. un patrón de comportamiento de crecimiento exponencial cambia a oscilatorio o a decrecimiento lineal).

- Sensibilidad en políticas: cambios en supuestos, frontera, nivel de agregación, parámetros o variables afectan significativamente las implicaciones para recomendaciones y diseño de políticas (las recomendaciones para definir cursos de acción para un tomador de decisión cambian).

Realice cambios en los valores de algunas variables, fracciones de nacimientos o "funciones tabla". Considere que estos cambios se hagan en intervalos sobre los que se considera aceptable que pueda variar el parámetro (no es aconsejable hacer cambios extremos pues esto corresponde a la prueba de condiciones extremas). Incluya los resultados en el Formato de control de experimentos en la columna de "Resultado post-simulación" para la simulación "5. Análisis de sensibilidad" para la variable correspondiente.

¿Qué tipos de sensibilidades presenta el modelo al cambiar los valores de algunas variables? ¿A qué tipos de cambios es más sensible el modelo? ¿Qué tipo de sensibilidad podría ser de interés para un tomador de decisión de este tipo de ecosistemas? Anote sus explicaciones u observaciones sobre el patrón de comportamiento de estas poblaciones en el Formato de registro de experimentos en la columna de "Observaciones/explicaciones/hipótesis" para la simulación "5. Análisis de sensibilidad" respectivamente para cada variable.

  1. Cambios en la frontera del modelo

Añada al modelo más aspectos que podrían ser de interés, los que prefiera (e.g. el nivel de comida disponible para los conejos, el agua, enfermedades, área dinámica, la invasión de una tercera especie, el impacto de asentamientos humanos, en fin, las posibilidades son muchas). Como se mencionó anteriormente, Vensim trae además una variedad de funciones para aprovechar, consulte el menú de ayuda del software. Suponga la información que necesite y anote sus estimaciones antes de correr el modelo en la columna de "Estimación (pre-simulación)" del Formato de control de experimentos, en la simulación "6. Cambios en la frontera" para la variable correspondiente.

Contraste sus estimaciones con el comportamiento de las poblaciones que se obtiene al simular. Incluya los resultados en el Formato de control de experimentos en la columna de "Resultado post-simulación" para la simulación "6. Cambios en la frontera" para la variable correspondiente.

Evalúe la sensibilidad en relación con los cambios introducidos. ¿Cómo afectan estos cambios de frontera el alcance del modelo? ¿Cómo decidir qué elementos incluir y qué elementos excluir en este modelo? En últimas, ¿para qué cree que puede servir este modelo? (más allá de hacer análisis y jugar con datos, gráficas y simulaciones). ¿Para qué propósitos puede ser útil el modelo? Anote sus explicaciones u observaciones sobre el patrón de comportamiento de estas poblaciones en el Formato de registro de experimentos en la columna de "Observaciones/explicaciones/hipótesis" para la simulación "6. Cambios en la frontera" respectivamente para cada variable.

Con esto ya cuenta con un modelo de la dinámica de zorros y conejos, así como también herramientas para analizar los resultados y la confiabilidad del modelo. Este tutorial estará disponible para que usted lo revise cuantas veces lo necesite.